Daily Compound Interest Calculator
Calculate the future value of an investment or debt where the principal is compounded daily. Enter the initial value, interest rate, and time period in days to find it.
Future Value:
| Total Interest: | $ |
Balance by Day
| Day | Balance | Interest Earned |
|---|---|---|
On this page:
Joseph Rich holds a Master's degree in finance and a Bachelor's degree in economics. He specializes in economics and investing analysis.
Laura started her career in Finance a decade ago and provides strategic financial management consulting. She has an MBA in Finance and a Bachelor's in Economics.
How to Calculate Daily Compound Interest
Daily compound interest is interest that is calculated daily on the principal and interest already accrued for an investment or loan. The daily compound interest calculator above is the easiest way to perform this calculation, but we will explain the steps in detail below.
It is important to note that the more frequent the compounding, the more interest will accrue. Daily compounded interest will result in more interest paid than interest compounded monthly or annually.
This is due to earning interest on interest or, in other words, compound interest. The faster you earn interest, the more your investment will grow, or in the case of debt, the more money you will have to repay.
The compounding that accrues the most interest is continuous compounding, and after that, the order from highest to lowest interest accrued is daily, monthly, quarterly, semiannually, and annually.
You can give this a try using our compound interest calculator to see the differences when using various methods of compounding.
Additionally, compound interest differs from simple interest in that interest is paid on interest that was previously accrued in addition to the principal. To calculate simple interest, try our simple interest calculator, which calculates interest that is only accrued based on the principal value.
Daily Compound Interest Formula
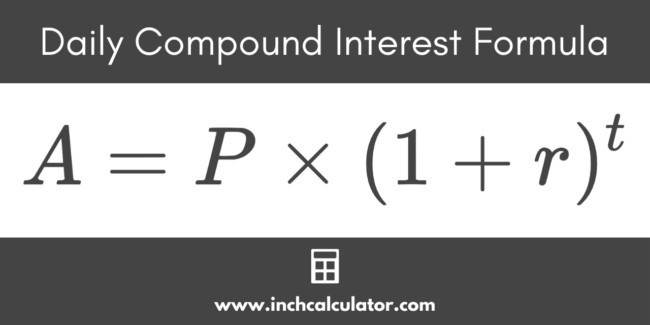
The daily compound interest formula is as follows:
A = P × (1 + r)t
where:
A = future value
P = principal value
r = daily interest rate
t = time in days
Note that the compounding occurs because we are raising 1 plus the interest rate r to the power of t. Under simple interest, the principal is multiplied by the interest rate so no compounding occurs.
This formula can also be applied for any time period. For example, let’s say you wanted to calculate monthly compound interest. In this case, you would multiply the daily interest rate by approximately 30.42 (or 365 days/12 months) and enter the number of months (as opposed to the number of days).
For example, let’s calculate daily compound interest if we invest $1,000 to earn 0.03% daily for 200 days. Using the daily compound interest formula above, we would start the equation as
$1,000 × (1 + 0.03%)200
$1,000 × 1.06183
$1,061.83
We can also select an annual interest rate in the daily compound interest calculator. To get the same result in the calculator using the annual interest rate, all we do is multiply the daily interest rate by 365.
So, using the previous example, the annual interest rate is 0.03% × 365 = 10.95%.
Use the prior assumptions of an initial value of $1,000 and 200 days, and now set the interest rate to “annual” and 10.95%. This will yield the exact same amount as the daily interest rate of 0.03%.
For example, let’s see how much would be gained by daily compounding as opposed to monthly compounding. We will change the assumptions slightly to make our calculation easier.
We can either earn 0.03% compounded daily for 365 days or 0.9125% compounded monthly for 12 months. We found the monthly interest rate by multiplying 0.03% by 365/12, but you can also use an interest rate calculator.
Daily Compounding
$1,000 × (1 + 0.03%)365
$1,000 × 1.11570
$1,115.70
Monthly Compounding
$1,000 × (1 + 0.9125%)12
$1,000 × 1.11517
$1,115.17
While only $0.53 in interest was gained by compounding daily, this is essentially free money that is earned because of more frequent compounding. Also, as the principal value gets larger and the time horizon gets longer, this amount will start to add up.
How to Find Daily Interest Rate from APR
The daily compound interest rate is easy to calculate once you have the APR (annual percentage rate). In fact, it is just the opposite of the calculation example in the prior section. All you need to do is divide the APR by 365. In the prior example, 10.95% was the APR and 0.03% was the daily interest rate.
For example, imagine you have a credit card with an APR of 15.90%. If we divide it by 365, we get a daily compound interest rate of 0.044%.
How to Account for Reinvestment
In the examples used here, we are assuming the investor leaves all the interest in the account to continue earning compounding interest. If the investor withdraws some of the interest, the future value will not be as large as we have calculated because the total value earning interest has decreased.
To account for reinvestment, you can re-apply the formula above for each reinvestment period to adjust the principal between each period.
Wrapping Up
As you can see, the more frequent the compounding, the more interest will be earned. Therefore, daily compounding yields more interest than monthly, quarterly, or annually compounded interest.
The daily interest calculator will calculate interest with either a daily interest rate or an annual interest rate. Just make sure that the correct interest rate and time period are used to calculate accurately.
Frequently Asked Questions
What type of investment accounts compound daily?
Certificates of deposit (CDs), money market accounts, and savings accounts may pay compound interest on a daily or monthly basis. Although the interest rate may be less than other investments, this adds up over time.
Do credit cards compound daily?
The majority of credit cards compound daily, so it’s important to understand the principal and interest payment each month and have a plan to pay it off.
Why is compound interest important?
Compound interest causes investments to grow faster, but also causes debt to grow faster. It’s important to understand what type of interest that you are earning on investments or accruing on debt so that you can properly plan for future earnings and payments.