Decimal to Binary Converter
Enter a decimal number below to convert it to a binary.
Binary Number:
Steps to Convert to Binary
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Pateakia has worked in education for 15 years and has three degrees, including a PhD, Master's degree, and Bachelor's degree. She specializes in mathematics.
How to Convert Decimal to Binary
The decimal number system is the number system most of us use every day. The decimal system, also referred to as denary, is a base 10 number system, which means it is composed of 10 digits, 0, 1, 2, 3, 4, 5, 6, 7, 8 & 9.
Binary numbers, also referred to as base 2 numbers, are the foundation of computing systems because they consist of only two digits, 0 and 1. This allows them to easily be used with electrical and mechanical switches. Binary numbers can also be used with modern transistors that make up modern computer processors.
You might be wondering how to convert from a decimal number to a binary number when these number systems do not use the same digits. To answer this, we need to dig in a little bit on how a binary number works.
A binary number is read from right to left, with the least significant bit being the digit on the far right end of the number and the most significant bit being the digit on the far left end.
Digit Values in a Binary Number
Each digit can be only a 1 or a 0, and digits that are a 1 are equivalent to 2n-1 where n is equal to the distance from the right side of the number.
This table shows the decimal values of the first nine digits in a binary number. Of course, a binary number can be much larger than nine digits, and the decimal value grows exponentially with each digit.
| MSB | Binary Digit | LSB | ||||||
|---|---|---|---|---|---|---|---|---|
| 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Steps to Convert
Now that you understand the representation of a base 2 number, you can convert from decimal to binary using successive division by 2. Whoa! I bet you’re probably wondering what that means!.
To use the successive division by two method, divide the decimal number by 2 using long division. There should be a remainder of 0 or 1; write that to the side of the division problem.
Take the result of the first division problem and divide that by 2 again. Like before, there should be a remainder of 0 or 1, which you should write to the side of the problem.
Continue this process until the result is 0.
The remainders that you wrote to the side of the division problems are the resulting binary number. The number should be read from the bottom to the top since the least significant digit will be at the top, and the most significant digit will be at the bottom.
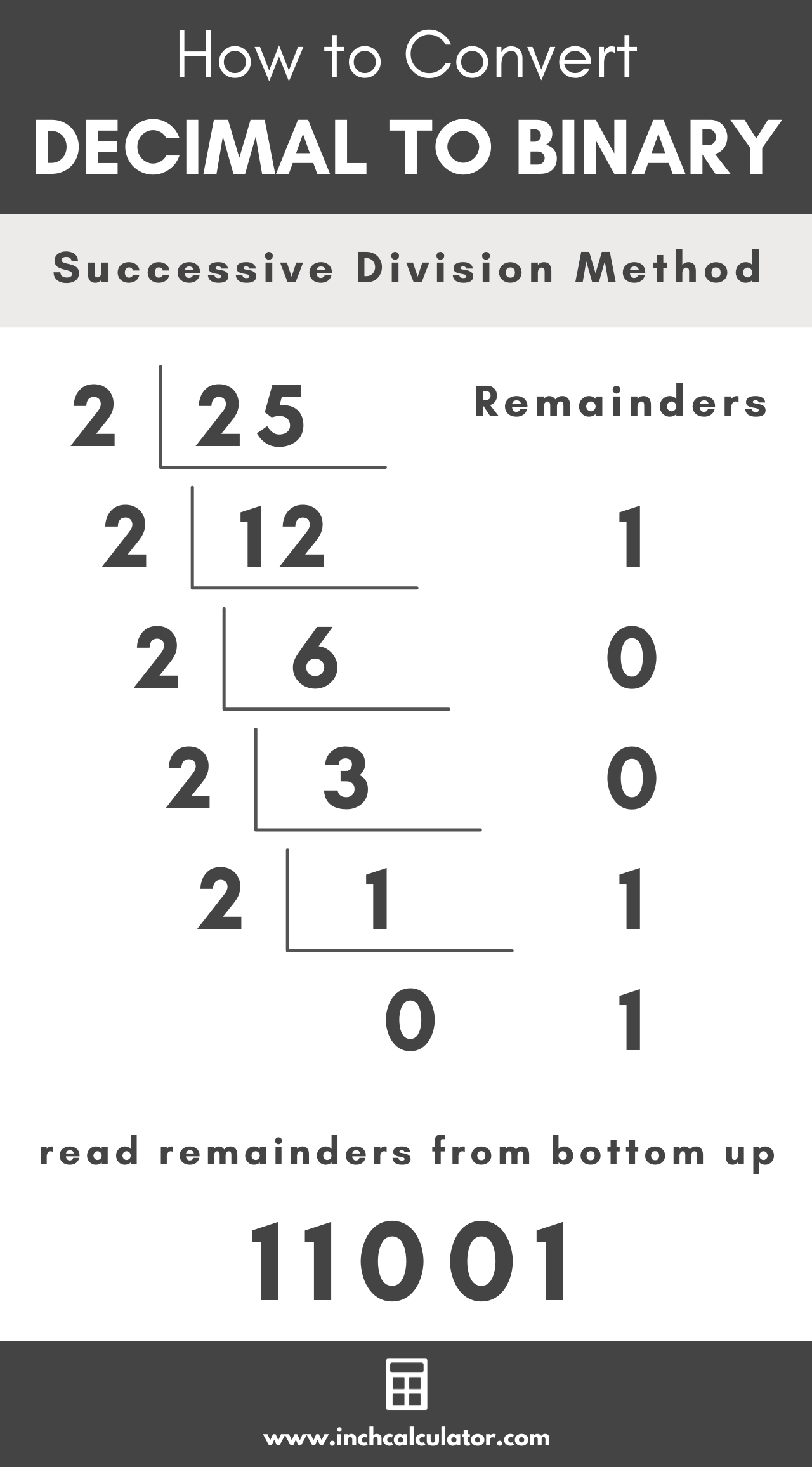
For example, let’s convert 25 from base 10 to base 2.
25 ÷ 2 = 12 R 1 (LSB)
12 ÷ 2 = 6 R 0
6 ÷ 2 = 3 R 0
3 ÷ 2 = 1 R 1
1 ÷ 2 = 0 R 1 (MSB)
Reading the remainders from the bottom up is 11001, so 2510 is equivalent to 110012.
Decimal to Binary Conversion Video Tutorial
Want to convert back to decimal to confirm your answer? Try our binary to decimal converter.
How to Convert a Fraction to Binary
To convert fractional decimal value to binary, multiply the fractional portion of the decimal by 2. If the result is greater than 1, then subtract 1 from the result and note that the binary bit will be a 1; otherwise, the binary bit will be a 0.
Continue multiplying by 2 until the resulting decimal value is equal to zero. The fractional result in binary is the remainder 0 and 1 values in order.
For example, let’s convert 0.25 from decimal to binary.
0.25 × 2 = 0.5 + 0
0.5 × 2 = 0 + 1
So, the fractional binary value is equal to 0.01
Decimal to Binary Conversion Table
The table below shows decimal numbers and the equivalent binary number values.
| Decimal Number | Binary Number |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
| 16 | 10000 |
| 17 | 10001 |
| 18 | 10010 |
| 19 | 10011 |
| 20 | 10100 |
| 21 | 10101 |
| 22 | 10110 |
| 23 | 10111 |
| 24 | 11000 |
| 25 | 11001 |
| 26 | 11010 |
| 27 | 11011 |
| 28 | 11100 |
| 29 | 11101 |
| 30 | 11110 |
| 31 | 11111 |
| 32 | 100000 |
| 64 | 1000000 |
| 128 | 10000000 |
| 256 | 100000000 |
| 512 | 1000000000 |
| 1024 | 10000000000 |
| 2048 | 100000000000 |
Frequently Asked Questions
What are the advantages of decimal to binary conversion?
Binary is easier for computers to store and manipulate, and the binary system is more efficient to use in mathematical operations.
When would you convert from decimal to binary?
You would convert decimal to binary when you have information that you need a computer system to process.
Is binary code still used?
Yes, binary code is still widely used and is the base of modern computer systems.