Fibonacci Sequence Calculator
Calculate the nth term in the Fibonacci sequence by entering the index n that you want to find.
Fibonacci Number:
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
What is the Fibonacci Sequence?
The Fibonacci sequence is a series of numbers where each number is equal to the sum of the previous two numbers in the sequence. Each number in the sequence is denoted as Fn, where n is the index of the number in the sequence.
The Fibonacci sequence starts with F0 and F1 equalling 0 and 1, respectively.
The Fibonacci sequence is often represented as a spiral, which is formed when creating squares with the width of each number in the sequence.
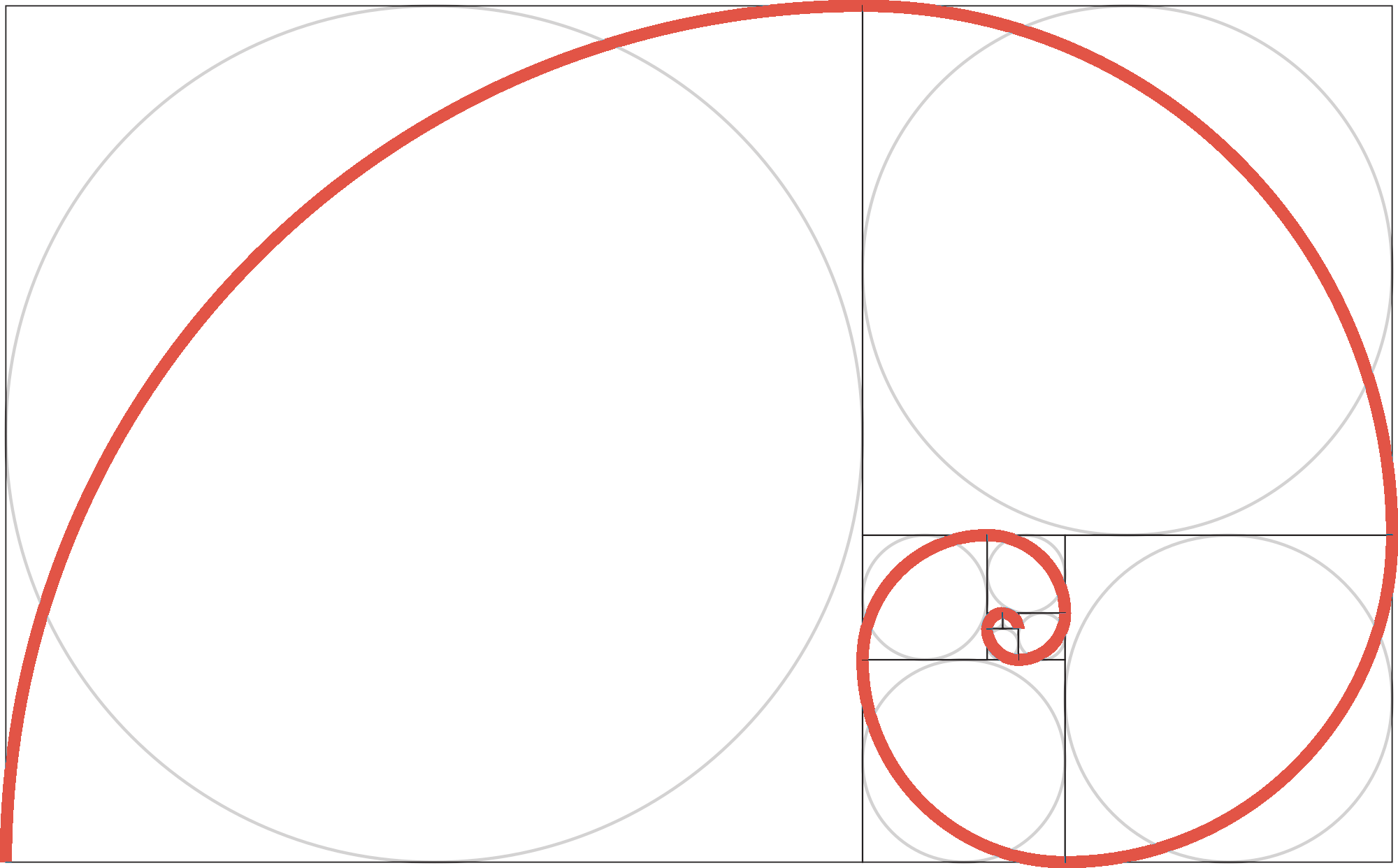
How to Calculate a Term in the Fibonacci Sequence
Because each term in the Fibonacci sequence is equal to the sum of the two previous terms, to solve for any term, it is required to know the two previous terms.
Formula to Solve the Nth Fibonacci Term
The equation to solve for any term in the sequence is:
Fn = Fn-1 + Fn-2
Thus, the Fibonacci term in the nth position is equal to the term in the nth minus 1 position plus the term in the nth minus 2 position.
Binet’s Formula
Named after French mathematician Jacques Philippe Marie Binet, Binet’s formula defines the equation to calculate the nth term in the Fibonacci sequence without using the recursive formula shown above.
Based on the golden ratio, Binet’s formula can be represented in the following form:
Fn = 1 / √5((1 + √5 / 2)n – (1 – √5 / 2)n)
Thus, Binet’s formula states that the nth term in the Fibonacci sequence is equal to 1 divided by the square root of 5, times 1 plus the square root of 5 divided by 2 to the nth power, minus 1 minus the square root of 5 divided by 2 to the nth power.
Binet’s formula above uses the golden ratio 1 + √5 / 2, which can also be represented as φ.
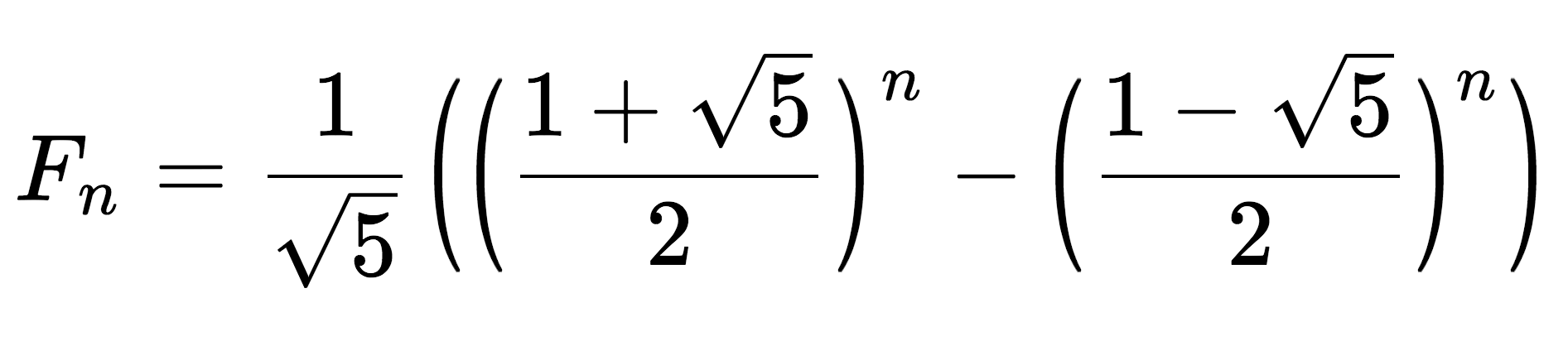
First 100 Numbers in the Fibonacci Sequence
The table below shows the first 100 numbers in the Fibonacci sequence.
| n | Fibonacci Number |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
| 8 | 21 |
| 9 | 34 |
| 10 | 55 |
| 11 | 89 |
| 12 | 144 |
| 13 | 233 |
| 14 | 377 |
| 15 | 610 |
| 16 | 987 |
| 17 | 1,597 |
| 18 | 2,584 |
| 19 | 4,181 |
| 20 | 6,765 |
| 21 | 10,946 |
| 22 | 17,711 |
| 23 | 28,657 |
| 24 | 46,368 |
| 25 | 75,025 |
| 26 | 121,393 |
| 27 | 196,418 |
| 28 | 317,811 |
| 29 | 514,229 |
| 30 | 832,040 |
| 31 | 1,346,269 |
| 32 | 2,178,309 |
| 33 | 3,524,578 |
| 34 | 5,702,887 |
| 35 | 9,227,465 |
| 36 | 14,930,352 |
| 37 | 24,157,817 |
| 38 | 39,088,169 |
| 39 | 63,245,986 |
| 40 | 102,334,155 |
| 41 | 165,580,141 |
| 42 | 267,914,296 |
| 43 | 433,494,437 |
| 44 | 701,408,733 |
| 45 | 1,134,903,170 |
| 46 | 1,836,311,903 |
| 47 | 2,971,215,073 |
| 48 | 4,807,526,976 |
| 49 | 7,778,742,049 |
| 50 | 12,586,269,025 |
| 51 | 20,365,011,074 |
| 52 | 32,951,280,099 |
| 53 | 53,316,291,173 |
| 54 | 86,267,571,272 |
| 55 | 139,583,862,445 |
| 56 | 225,851,433,717 |
| 57 | 365,435,296,162 |
| 58 | 591,286,729,879 |
| 59 | 956,722,026,041 |
| 60 | 1,548,008,755,920 |
| 61 | 2,504,730,781,961 |
| 62 | 4,052,739,537,881 |
| 63 | 6,557,470,319,842 |
| 64 | 10,610,209,857,723 |
| 65 | 17,167,680,177,565 |
| 66 | 27,777,890,035,288 |
| 67 | 44,945,570,212,853 |
| 68 | 72,723,460,248,141 |
| 69 | 117,669,030,460,994 |
| 70 | 190,392,490,709,135 |
| 71 | 308,061,521,170,129 |
| 72 | 498,454,011,879,264 |
| 73 | 806,515,533,049,393 |
| 74 | 1,304,969,544,928,657 |
| 75 | 2,111,485,077,978,050 |
| 76 | 3,416,454,622,906,707 |
| 77 | 5,527,939,700,884,757 |
| 78 | 8,944,394,323,791,464 |
| 79 | 14,472,334,024,676,221 |
| 80 | 23,416,728,348,467,685 |
| 81 | 37,889,062,373,143,906 |
| 82 | 61,305,790,721,611,591 |
| 83 | 99,194,853,094,755,497 |
| 84 | 160,500,643,816,367,088 |
| 85 | 259,695,496,911,122,585 |
| 86 | 420,196,140,727,489,673 |
| 87 | 679,891,637,638,612,258 |
| 88 | 1,100,087,778,366,101,931 |
| 89 | 1,779,979,416,004,714,189 |
| 90 | 2,880,067,194,370,816,120 |
| 91 | 4,660,046,610,375,530,309 |
| 92 | 7,540,113,804,746,346,429 |
| 93 | 12,200,160,415,121,876,738 |
| 94 | 19,740,274,219,868,223,167 |
| 95 | 31,940,434,634,990,099,905 |
| 96 | 51,680,708,854,858,323,072 |
| 97 | 83,621,143,489,848,422,977 |
| 98 | 135,301,852,344,706,746,049 |
| 99 | 218,922,995,834,555,169,026 |
| 100 | 354,224,848,179,261,915,075 |