Normal Force Calculator
Use our normal force calculator to find the normal force exerted on an object given its mass and the angle of the surface.
Normal Force:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
How to Find Normal Force
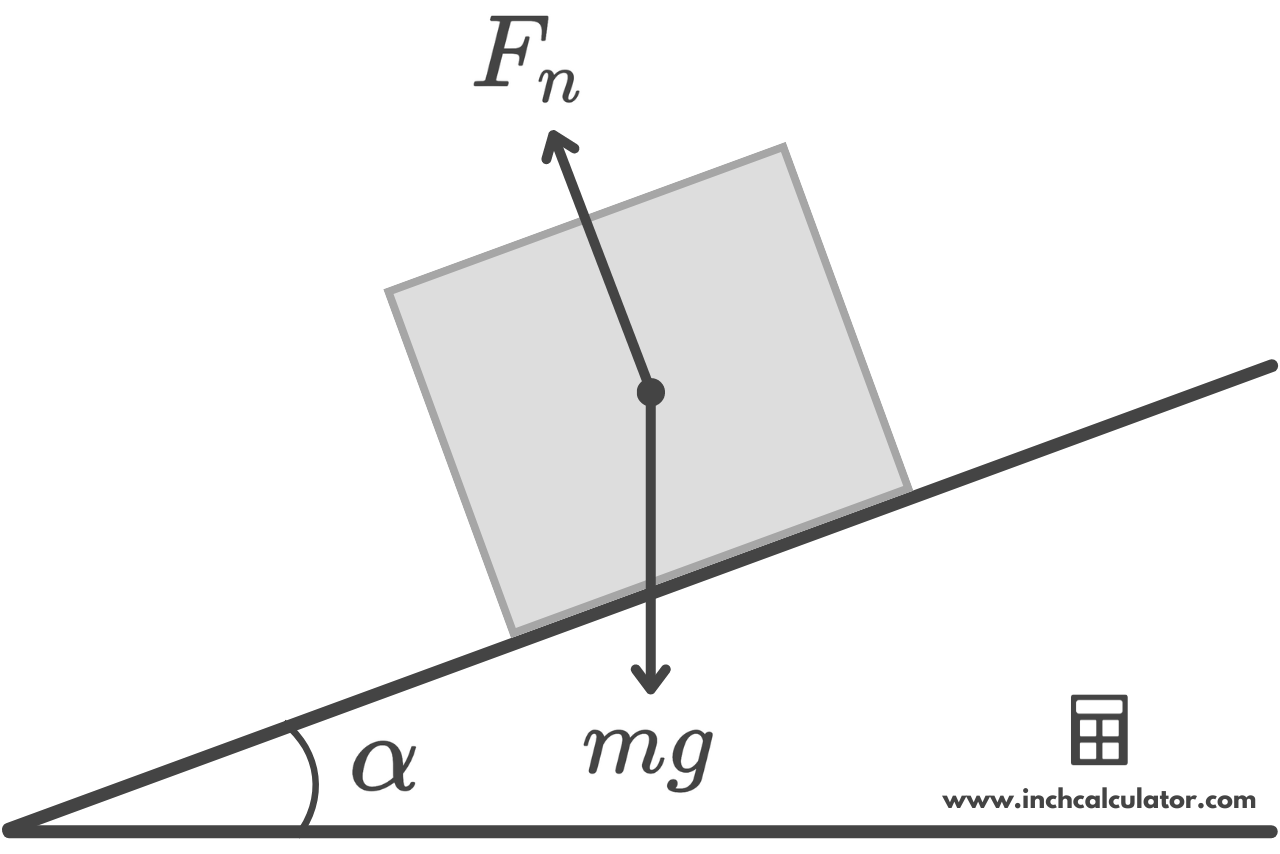
Normal force (denoted as Fn) is essential for understanding how objects interact with surfaces. It is not an inherent force that an object possesses but rather a reactive force exerted by a surface when an object presses against it.
This force is a direct consequence of Newton’s Third Law of Motion, which states that for every action, there is an equal and opposite reaction.
When an object rests on a horizontal surface without accelerating, the normal force counteracts the object’s weight (the force due to gravity), and the two forces balance each other out. However, if the surface is inclined or if additional forces are applied (like pushing down on the object), calculating the normal force becomes slightly more complex.
Normal Force Equation
You can calculate the normal force exerted on an object using the following formula:
Where:
Fn = normal force
m = object’s mass
g = gravitational force (9.80665 m/s² on Earth)
α = angle of the surface
Thus, normal force is equal to the mass of the object m times the gravitational force g times the cosine of the surface angle α.
If the object is sitting on a flat surface, then the normal force is simply equal to m times g.
For example, let’s calculate the normal force exerted on a box with a mass of 10 kg resting on a plane inclined at an angle of 30 degrees to the horizontal.
Thus, the normal force exerted by the inclined plane on the box is approximately 84.868 Newtons.