SOHCAHTOA Calculator
Use our SOHCAHTOA calculator to solve a right triangle using the SOH·CAH·TOA method.
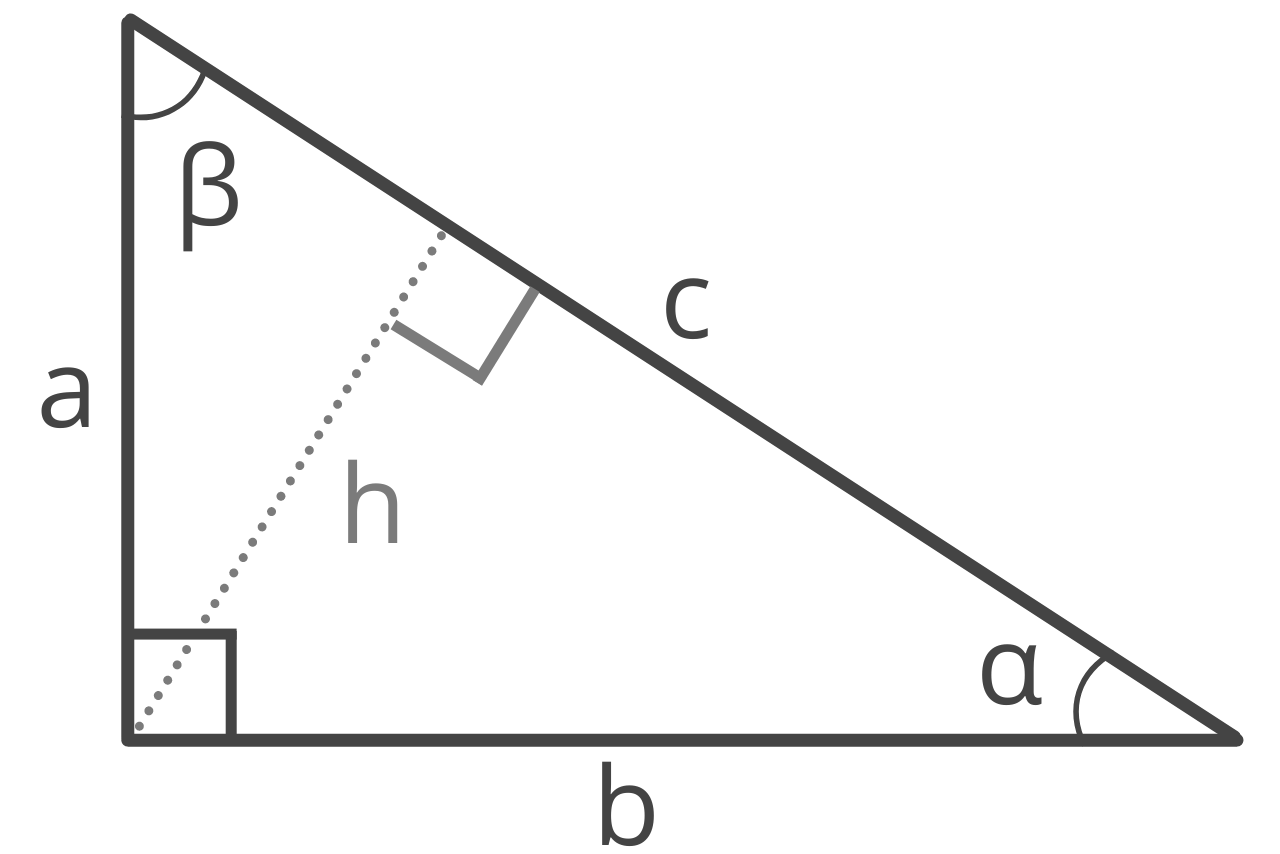
Right Triangle Properties:
| leg a: | 5
|
| leg b: | 12
|
| hypotenuse c: | 13
|
| angle α: | |
| angle β: | |
| height h: | 4.615
|
| area: | 30
|
| perimeter: | 30
|
| inradius: | 2
|
| circumradius: | 6.5
|
On this page:
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Dr. Connor Smith is a professor of electrical and computer engineering with expertise in electromagnetics, microsystems, and magnetic materials and devices.
How to Solve Right Triangles Using SOHCAHTOA
A right triangle is a triangle with a right interior angle equal to 90 degrees. The trigonometric functions sine, cosine, and tangent allow you to solve the properties of this special triangle.
If you know the lengths of two sides of a right triangle, then you can solve the interior angles using these trigonometric functions.
To find an angle when given two side lengths, you can use the following formulas:
sin(θ) = opposite / hypotenuse
cos(θ) = adjacent / hypotenuse
tan(θ) = opposite / adjacent
SOHCAHTOA is a mnemonic device to help remember these equations used for solving for the properties of a right triangle.
In these expressions, the opposite side is the side that is opposite to the acute angle θ, the adjacent side is the shorter side adjacent to the acute angle, and the hypotenuse is the longest side of the right triangle that is opposite to the 90-degree right angle.
SOHCAHTOA refers to three different expressions, each representing one of the formulas, where each letter is the first letter in the parts of the equation.
SOH · CAH · TOA
SOH: sin(θ) = opposite ÷ hypotenuse
CAH: cos(θ) = adjacent ÷ hypotenuse
TOA: tan(θ) = opposite ÷ adjacent
The first part of the SOHCAHTOA mnemonic (SOH) refers to the expression where the sine of the angle θ is equal to the length of the side opposite to the angle divided by the hypotenuse.
The second part of SOHCAHTOA (CAH) refers to the expression where the cosine of the angle θ is equal to the length of the side adjacent to the angle divided by the hypotenuse.
The final part of SOHCAHTOA (TOA) refers to the expression where the tangent of the angle θ is equal to the length of the side opposite to the angle divided by the length of the side adjacent to the angle.
SOHCAHTOA Table
The following table shows the three formulas that make up SOHCAHTOA.
| SOH | sin(θ) = opposite / hypotenuse |
|---|---|
| CAH | cos(θ) = adjacent / hypotenuse |
| TOA | tan(θ) = opposite / adjacent |
Frequently Asked Questions
Is SOHCATOA the same as the Pythagorean theorem?
Not quite. The Pythagorean theorem relates the three sides of a right triangle, while SOHCAHTOA is a mnemonic that is used to remember the relationship between the acute angles in a right triangle and the length of the sides.
Can you use SOHCATOA for non-right triangles?
No, the SOHCATOA mnemonic refers to the relationship between the acute angles in a right triangle and the length of the sides, but it cannot be used for triangles that do not have a right angle.
What is CHOSHACAO?
CHOSHACAO is another mnemonic to remember the reciprocals of the formulas used in SOHCAHTOA.
The first part of the CHOSHACAO mnemonic (CHO) refers to the expression where the cosecant of the angle θ is equal to the length of the hypotenuse divided by the length of the side opposite to the angle. This is the reciprocal of the SOH portion of SOHCAHTOA.
The second part of CHOSHACAO (SHA) refers to the expression where the secant of the angle θ is equal to the length of the hypotenuse divided by the length of the side adjacent to the angle. This is the reciprocal of the CAH portion of SOHCAHTOA.
The final part of CHOSHACAO (CAO) refers to the expression where the cotangent of the angle θ is equal to the length of the side adjacent to the angle divided by the length of the side opposite to the angle. This is the reciprocal of the TOA portion of SOHCAHTOA.
| CHO | csc(θ) = hypotenuse / opposite |
|---|---|
| SHA | sec(θ) = hypotenuse / adjacent |
| CAO | cot(θ) = adjacent / opposite |