Voltage Drop Calculator
Calculate voltage drop in an AC or DC circuit given wire gauge, voltage, current, and length. You can also determine the correct conductor size and length for a circuit given an allowable voltage drop.
Voltage Drop:
| In Volts: | 0 volts
|
| As a Percentage: | 0%
|
| End of Circuit Voltage: | 0 volts
|
Conductor Diameter
| inches: | 0 in
|
| millimeters: | 0 mm
|
Conductor Cross-sectional Area
| kcmil: | 0 kcmil
|
| square inches: | 0 in2
|
| square millimeters: | 0 mm2
|
Expected Voltage Drop
| feet | |
| meters |
On this page:
How to Calculate Voltage Drop
Voltage drop is the amount of voltage lost in a circuit due to the resistance of the conductor. Voltage drop is an important consideration when planning a circuit to allow equipment using the circuit to run as designed.
Voltage drop in a circuit means less voltage is delivered to connected devices. Electrical devices consume power, and when they get reduced voltages, the current flow increases to meet their power needs. This current increase can overheat the circuit, causing damage to the equipment and devices.
Using Ohm’s Law, the voltage can be calculated by multiplying the current by the resistance.
V(V) = I(A) × R(Ω)
Ohm’s Law states that the voltage is equal to the product of the current and the resistance. You can find the resistance for various conductor sizes in the chart below, or use one of the following voltage drop formulas.
Voltage Drop Formula
Thus, you can calculate voltage drop for single-phase AC and DC circuits using the following formula derived from Ohm’s Law:[1]
Vdrop (V) = 2 × I(A) × ρ(Ω·m) × L(m) / Am²
Where:
V = allowable voltage drop in volts
I = current in amps
ρ = conductor resistivity in ohm-meters (Ω·m)
L = conductor length in meters
A = conductor cross-sectional area in square meters
So, the voltage drop V in volts is equal to twice the product of the current I in amps, the conductor resistivity ρ in ohm-meters, and the conductor length L in meters, divided by the cross-sectional area of the conductor A in square meters.
The resistivity of copper conductors is 1.7241 × 10-8 Ω·m and the resistivity of aluminum conductors is 2.6548 × 10-8 Ω·m. Since copper has lower resistivity than aluminum, the voltage drop across a copper wire would be lower than an aluminum wire, for a given length and cross-sectional area.
Alternate Voltage Drop Formula
You may also see voltage drop calculated using an alternate formula, which calculates the conductor resistance in a slightly different way:[2]
Vdrop (V) = I(A) × 2 × K × L(m) / Amm²
Where:
V = allowable voltage drop in volts
K = direct current constant – use 12.9 for copper conductors and 21.2 for aluminum conductors. This is equal to the resistance of a conductor that is one thousand circular mils in area and one thousand feet in length.
I = current in amps
L = conductor length in meters
A = conductor cross-sectional area in square millimeters
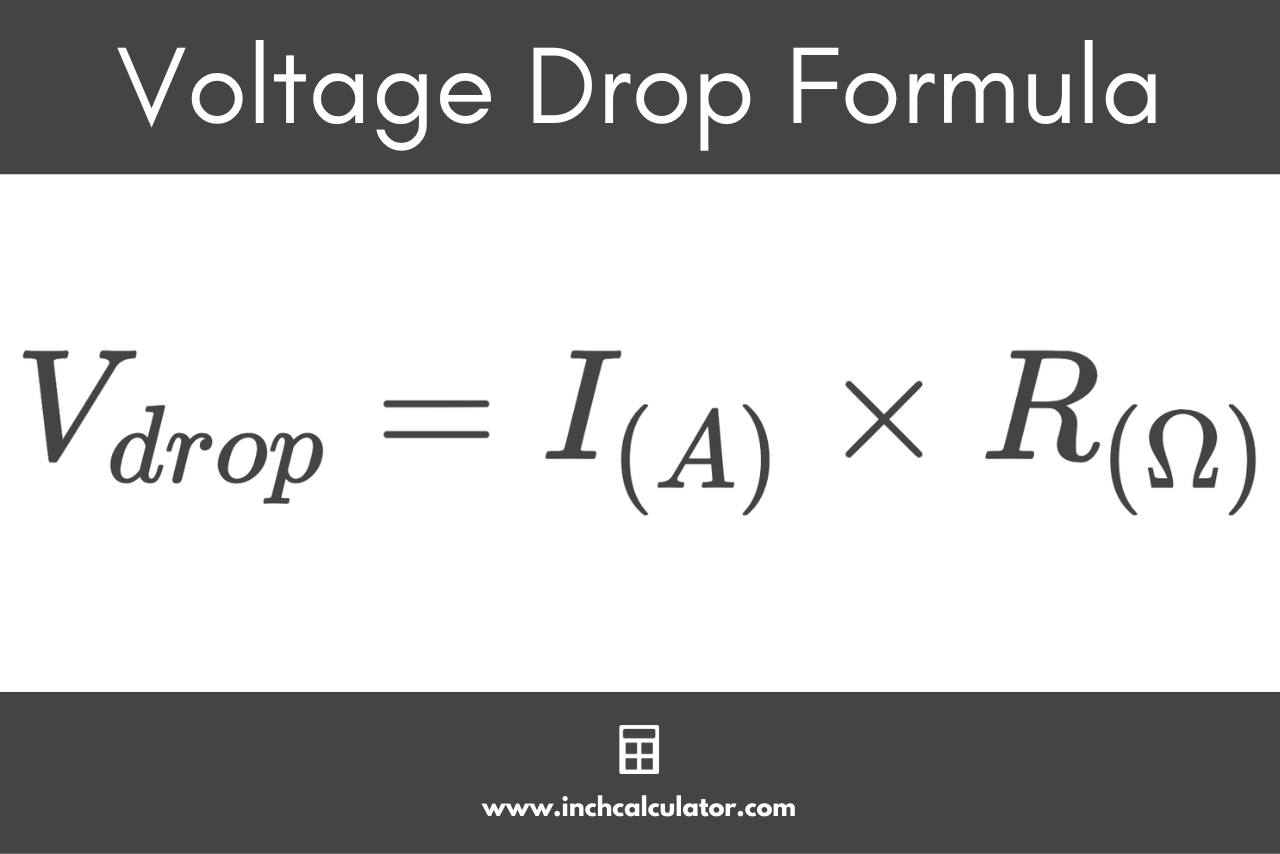
For example: let’s calculate the voltage drop of a 120V circuit drawing 15A using a 25′ long 14AWG (American Wire Gauge) copper conductor.
A 14 AWG wire has a cross-sectional area of 2.081 mm² per the table below, and you can convert this to square meters by multiplying by 1,000,000. Recall that the resistivity of a copper conductor is 1.7241×10-8 Ω·m. You can convert the length in feet to meters by multiplying by 0.3048.
Vdrop (V) = 2 × 15A × 1.7241×10-8 × (25 ft × 0.3048 m⁄ft) / 2.081 m² × 1,000,000
Vdrop (V) = 1.894 V
So, we can expect a voltage drop of 1.894 volts in this circuit.
Voltage Drop Formula for Three-Phase Systems
The formula to calculate voltage drop in three-phase systems is
Vdrop (V) = √3 × I(A) × ρ(Ω·m) × L(m) / Am²
In a three-phase system, the voltage drop V in volts is equal to the square root of 3 times the product of the current I in amps, the conductor resistivity ρ in ohm-meters, and the conductor length L in meters, divided by the cross-sectional area of the conductor A in square meters.
How to Calculate the Minimum Conductor Size
Depending on the application, it is important to use conductors of the proper cross-sectional area for economical and reliable power delivery. A large conductor would be a waste of money, and an undersized conductor might not be able to handle the required current flows.
Using the equation for voltage drop and rearranging the variables, the minimum conductor size in square meters for a circuit can be found using the following:
A(m²) = 2 × ρ(Ω·m) × L(m) × I(A) / Vdrop (V)
Where:
A = cross-sectional area in square meters
ρ = conductor resistivity in ohm-meters (Ω·m)
L = length in meters
I = current in amps
Vdrop = allowable voltage drop in volts
The minimum cross-sectional area A for a conductor in square meters is equal to twice the product of the conductor resistivity ρ in ohm-meters, the conductor length L in meters, and the current I in amps, divided by the maximum allowable voltage drop V in volts.
You can multiply the resulting cross-sectional area by 1,000,000 to calculate the area in square millimeters. Then, use our wire size calculator to find the wire gauge with the correct cross-sectional area.
You’ll also need to consider the current rating when determining the minimum conductor size. The National Electric Code has several tables to determine the maximum allowable current for a conductor. You can also use our wire ampacity calculator to calculate the maximum current rating for a conductor.
You should always consult with an electrician or electrical professional when choosing your wire to ensure it meets the code requirements and will work safely for your application.
For example: let’s find the minimum wire gauge needed for a 120V circuit drawing 20A using a 40′ long copper conductor with a max voltage drop of 3%.
A 3% voltage drop would be 3.6 volts. Recall that the resistivity of a copper conductor is 1.7241×10-8 Ω·m. You can convert the length in feet to meters by multiplying by 0.3048.
A(m²) = 2 × 1.7241×10-8 × (40 ft × 0.3048 ft⁄m) × 20A / 3.6V
A(m²) = 2 × 1.7241×10-8 × 12.192 m × 20A / 3.6V
A(m²) = 8.408×10-6 / 3.6V
A(m²) = 2.3356×10-6m²
Then, multiply by 1,000,000 to convert the cross-sectional area in square meters to square millimeters.
A(mm²) = 2.3356×10-6 m² × 1,000,000
A(mm²) = 2.3356 mm²
Finally, refer to the table below to find the minimum wire gauge for this cross-sectional area. From the table, the wire gauge required for a cross-sectional area of 2.081 mm² is 14 AWG and the wire gauge required for a cross-sectional area of 2.624 mm² is 13 AWG. So, the minimum wire gauge required for our example (cross-sectional area of 2.3356 mm²) is 13 AWG.
How to Calculate the Maximum Conductor Length
It is essential to use conductors of proper lengths to ensure minimal voltage drop in the conductive element. A longer conductor means the current must travel a longer distance through the conductive material and against more resistance.
This increase in resistance produces more voltage drops across the length of the circuit and causes it to overheat.
The maximum length of a conductor in a circuit can be determined by re-writing the formula for voltage drop like this:
L(m) = Vdrop (V) × Am² / 2 × ρ(Ω·m) × I(A)
Where:
Vdrop = allowable voltage drop in volts
I = current in amps
ρ = conductor resistivity in ohm-meters (Ω·m)
L = conductor length in meters
A = conductor cross-sectional area in square meters
The maximum conductor length is equal to the product of the maximum allowable voltage drop Vdrop in volts and the cross-sectional area of the conductor in square meters, divided by twice the product of the conductor resistivity ρ in ohm-meters and the current I in amps.
Conductor Size and Resistance Table
| AWG | Cross-Sectional Area | Resistance | ||
|---|---|---|---|---|
| (kcmil) | (mm²) | Ohms per 1000ft | Ohms per 1000m | |
| 0000 (4/0) | 211.6 | 107.22 | 0.049 | 0.1608 |
| 000 (3/0) | 167.81 | 85.029 | 0.0618 | 0.2028 |
| 00 (2/0) | 133.08 | 67.431 | 0.0779 | 0.2557 |
| 0 (1/0) | 105.53 | 53.475 | 0.0983 | 0.3224 |
| 1 | 83.693 | 42.408 | 0.1239 | 0.4066 |
| 2 | 66.371 | 33.631 | 0.1563 | 0.5127 |
| 3 | 52.635 | 26.67 | 0.197 | 0.6464 |
| 4 | 41.741 | 21.151 | 0.2485 | 0.8152 |
| 5 | 33.102 | 16.773 | 0.3133 | 1.028 |
| 6 | 26.251 | 13.302 | 0.3951 | 1.296 |
| 7 | 20.818 | 10.549 | 0.4982 | 1.634 |
| 8 | 16.51 | 8.366 | 0.6282 | 2.061 |
| 9 | 13.093 | 6.634 | 0.7921 | 2.599 |
| 10 | 10.383 | 5.261 | 0.9988 | 3.277 |
| 11 | 8.234 | 4.172 | 1.26 | 4.132 |
| 12 | 6.53 | 3.309 | 1.588 | 5.211 |
| 13 | 5.178 | 2.624 | 2.003 | 6.571 |
| 14 | 4.107 | 2.081 | 2.525 | 8.285 |
| 15 | 3.257 | 1.65 | 3.184 | 10.448 |
| 16 | 2.583 | 1.309 | 4.015 | 13.174 |
| 17 | 2.048 | 1.038 | 5.063 | 16.612 |
| 18 | 1.624 | 0.823 | 6.385 | 20.948 |
| 19 | 1.288 | 0.6527 | 8.051 | 26.415 |
| 20 | 1.022 | 0.5176 | 10.152 | 33.308 |
| 21 | 0.8101 | 0.4105 | 12.802 | 42.001 |
| 22 | 0.6424 | 0.3255 | 16.143 | 52.962 |
| 23 | 0.5095 | 0.2582 | 20.356 | 66.784 |
| 24 | 0.404 | 0.2047 | 25.668 | 84.213 |
| 25 | 0.3204 | 0.1624 | 32.367 | 106.19 |
| 26 | 0.2541 | 0.1288 | 40.814 | 133.9 |
| 27 | 0.2015 | 0.1021 | 51.466 | 168.85 |
| 28 | 0.1598 | 0.081 | 64.897 | 212.92 |
| 29 | 0.1267 | 0.0642 | 81.833 | 268.48 |
| 30 | 0.1005 | 0.0509 | 103.19 | 338.55 |
| 31 | 0.0797 | 0.0404 | 130.12 | 426.9 |
| 32 | 0.0632 | 0.032 | 164.08 | 538.32 |
| 33 | 0.0501 | 0.0254 | 206.9 | 678.8 |
| 34 | 0.0398 | 0.0201 | 260.9 | 855.96 |
| 35 | 0.0315 | 0.016 | 328.98 | 1,079.3 |
| 36 | 0.025 | 0.0127 | 414.84 | 1,361 |
| 37 | 0.0198 | 0.01 | 523.1 | 1,716.2 |
| 38 | 0.0157 | 0.007967 | 659.62 | 2,164.1 |
| 39 | 0.0125 | 0.006318 | 831.77 | 2,728.9 |
| 40 | 0.009888 | 0.00501 | 1,048.8 | 3,441.1 |
Also check out our electricity cost calculator to see how much it will cost to power a device.
References
- LibreTexts - Physics, University Physics II - Thermodynamics, Electricity, and Magnetism - 9.4: Resistivity and Resistance, https://phys.libretexts.org/Bookshelves/University_Physics/Book%3A_University_Physics_(OpenStax)/Book%3A_University_Physics_II_-_Thermodynamics_Electricity_and_Magnetism_(OpenStax)/09%3A_Current_and_Resistance/9.04%3A_Resistivity_and_Resistance
- IAEI Magazine, Voltage Drop Formulas, https://iaeimagazine.org/electrical-fundamentals/voltage-drop-formulas/





