Volume Calculator
Calculate volume by selecting one of the shapes below and entering your measurements in any unit.
Volume:
On this page:
- Volume Calculator - Find Volume
- How to Find Volume
- Volume Formulas
- Volume of a Cube
- Volume of a Rectangular Prism
- Volume of a Sphere
- Volume of a Cylinder
- Volume of a Cone
- Volume of a Pyramid
- Volume of a Triangular Prism
- Volume of a Capsule
- Volume of a Hemisphere
- Volume of a Spherical Cap
- How to Find the Volume of an Irregular Object
- Measuring Volume Using Weight
- Volume Measurement Tips
- Common Volume Measurements
- Frequently Asked Questions
Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Pateakia has worked in education for 15 years and has three degrees, including a PhD, Master's degree, and Bachelor's degree. She specializes in mathematics.
How to Find Volume
Volume is the measure of 3-dimensional space that a geometric shape or object occupies. It’s measured in cubic units, such as cubic yards or cubic feet.
Of course, you can find volume easily using a calculator like the one above, but you can also find it by using a formula. Read on to learn more about how to calculate volume yourself.
Volume Formulas
The volume of every shape is calculated differently using a different formula. Below you will find the formulas to find the volume of several three-dimensional shapes.
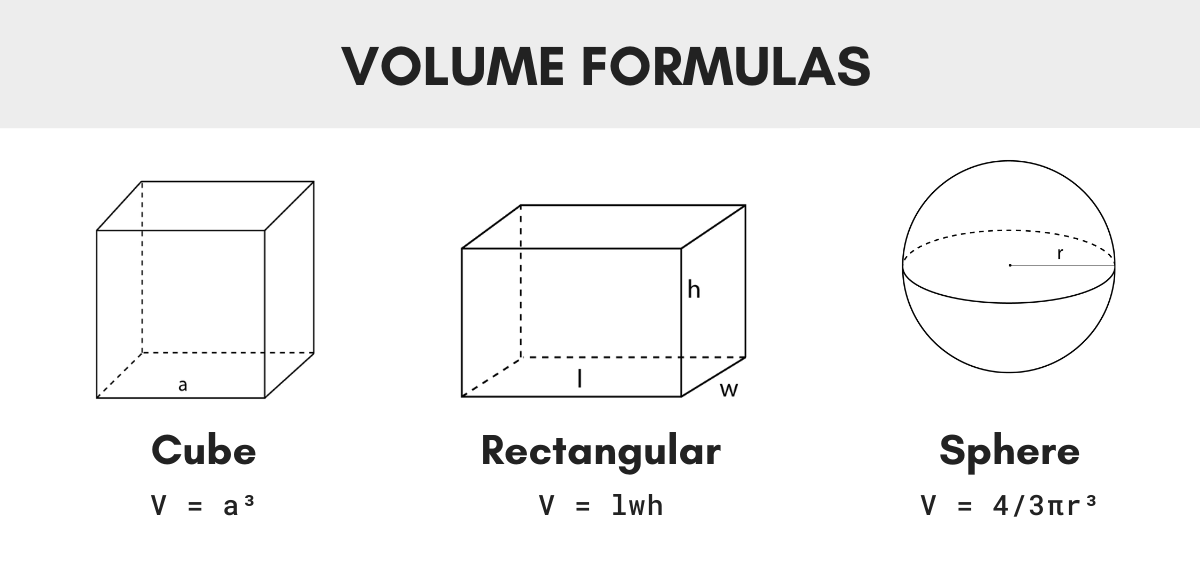
Volume of a Cube
V = a3
a = edge a length
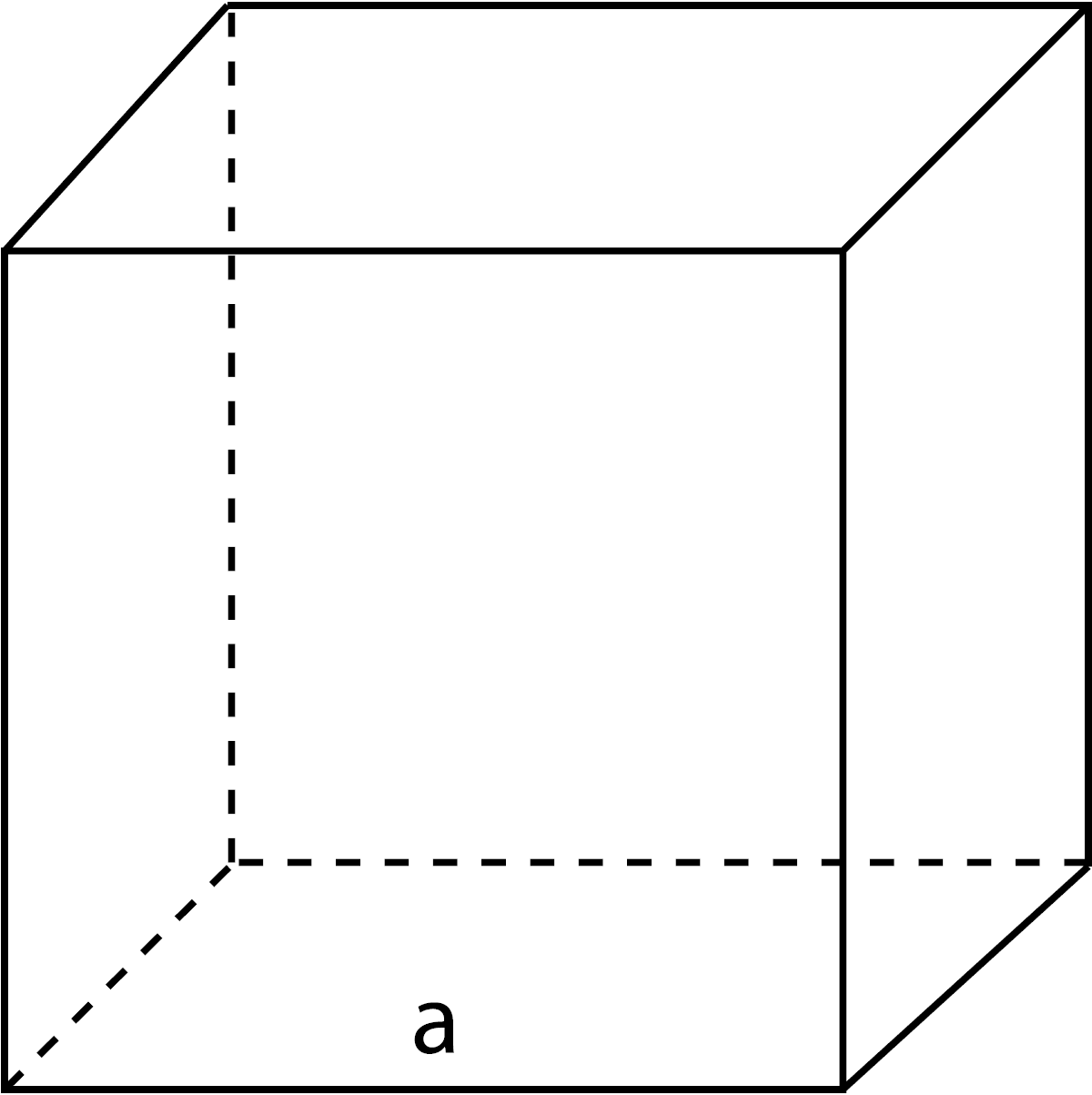
Volume of a Rectangular Prism
V = l × w × h
l = length
w = width
h = height
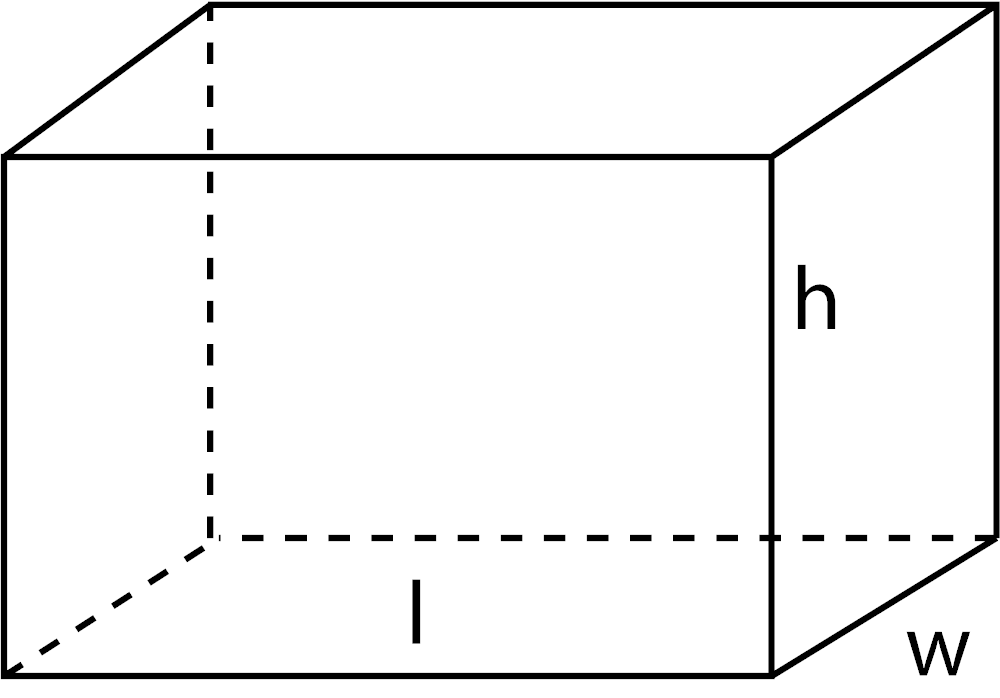
Volume of a Sphere
V = 4 / 3πr3
r = radius
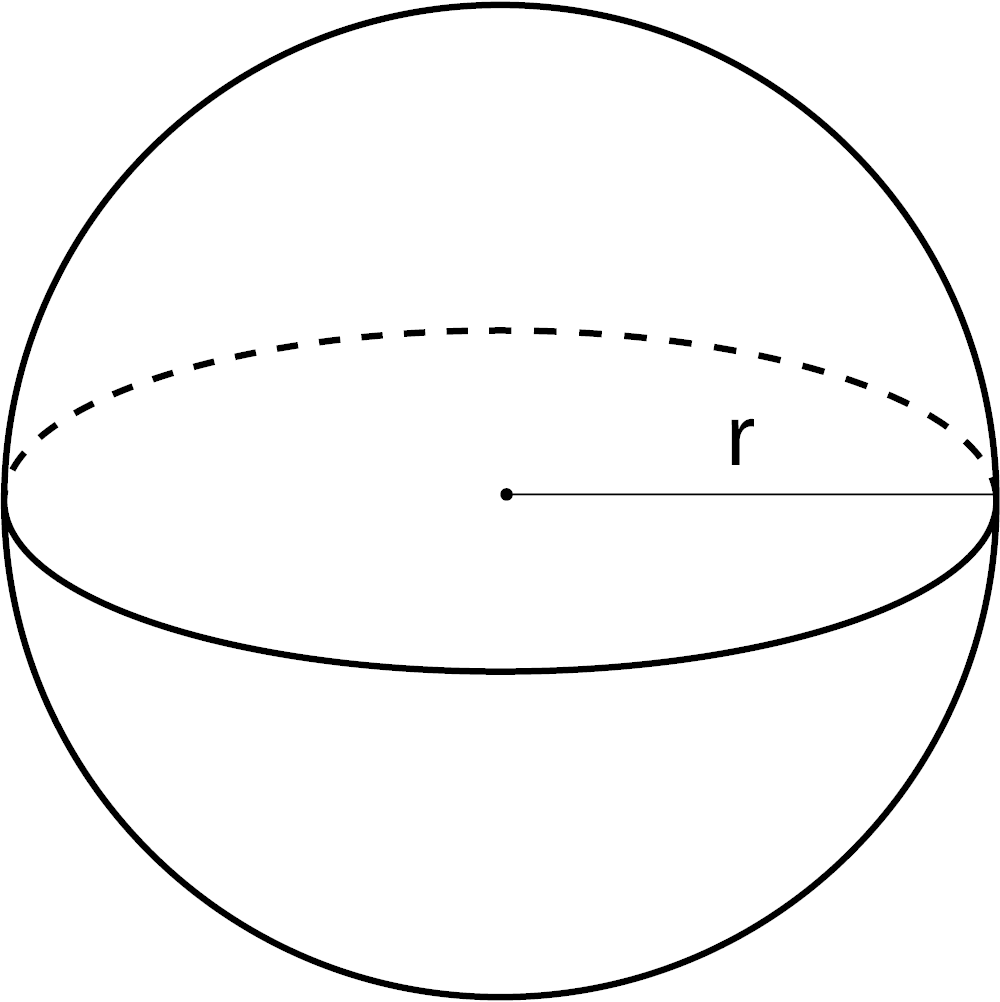
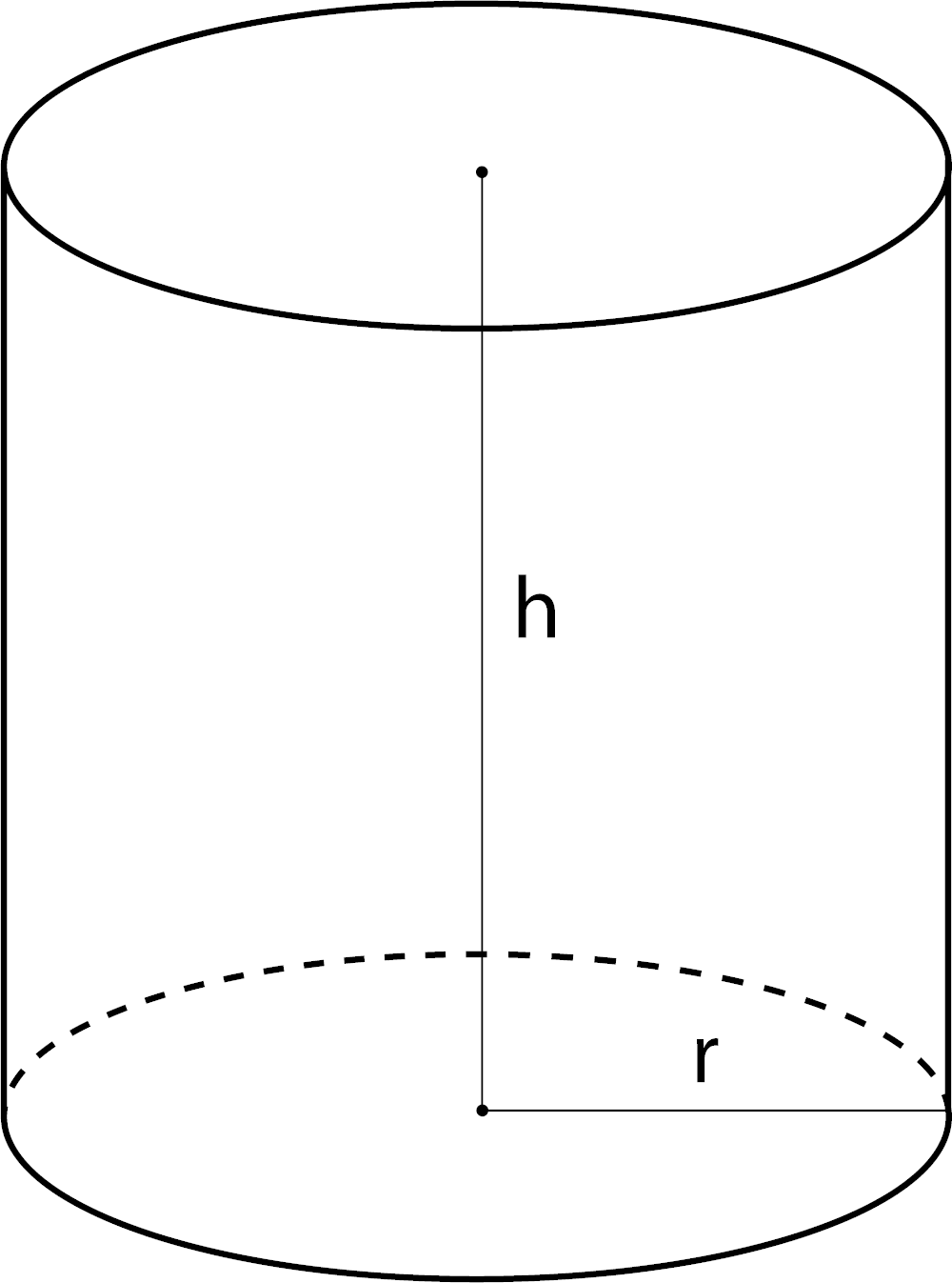
Volume of a Cylinder
V = πr2h
r = radius
h = height
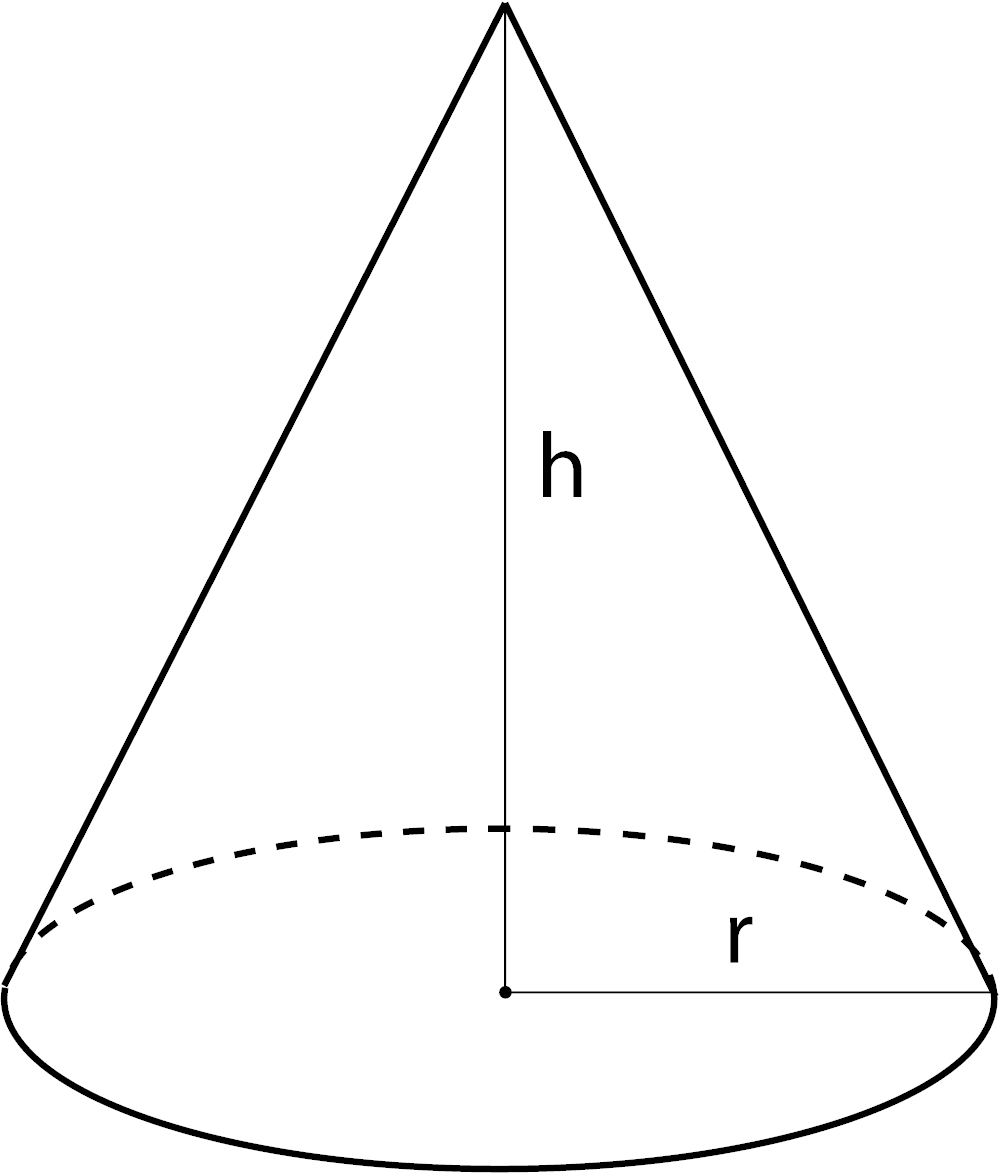
Volume of a Cone
V = 1 / 3πr2h
r = radius
h = height
You can also use our cone volume calculator to solve this.
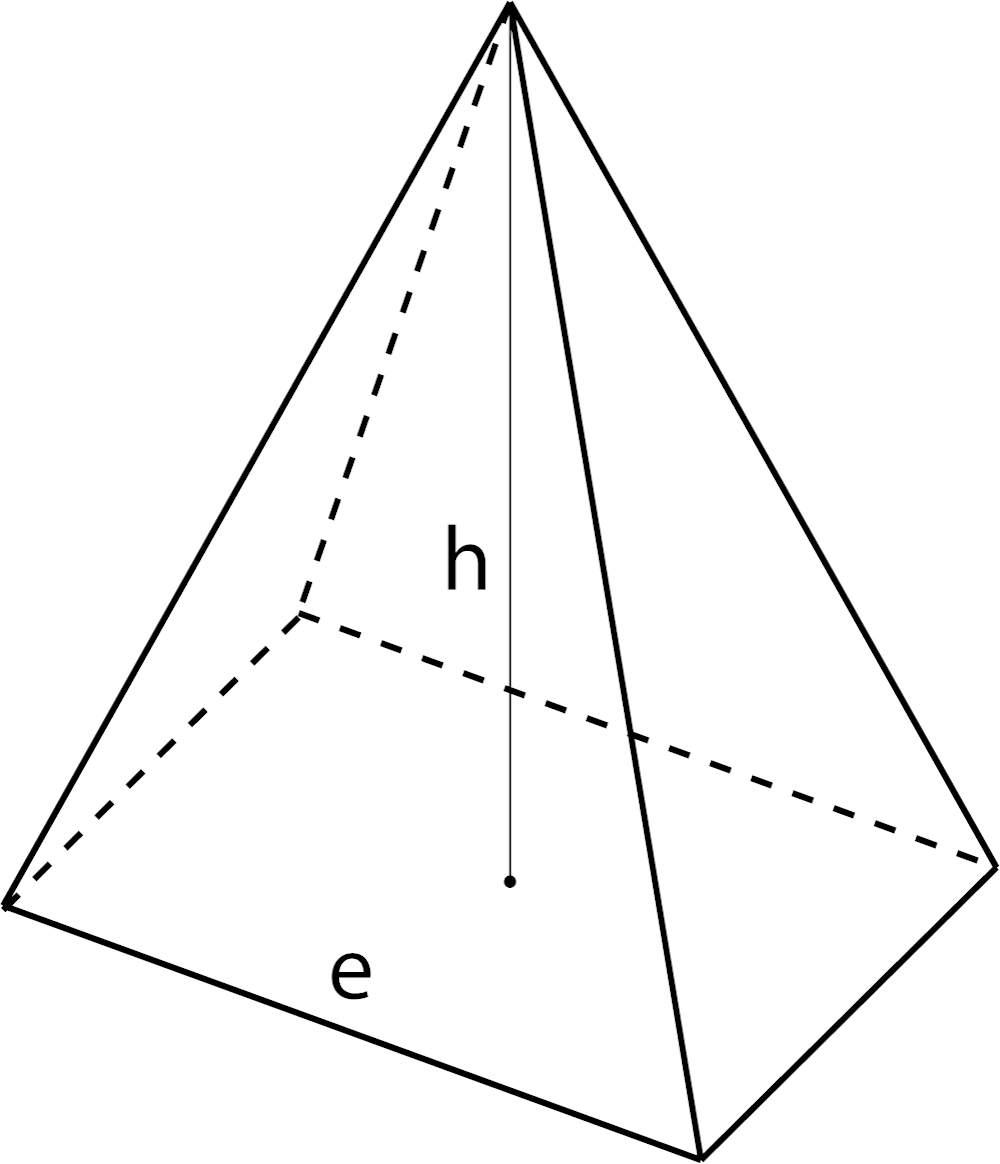
Volume of a Pyramid
V = 1 / 3e2h
e = edge length
h = height
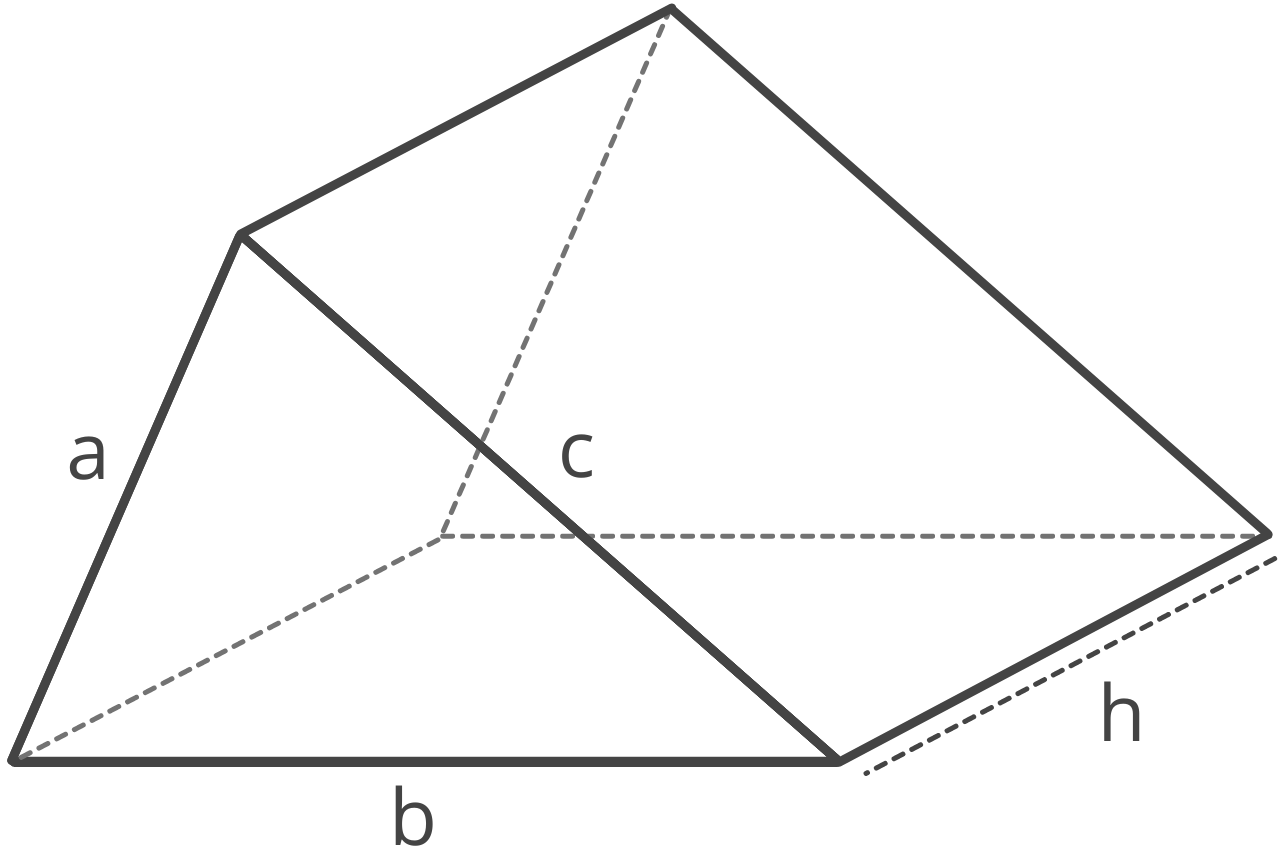
Volume of a Triangular Prism
s = 1/2(a + b + c)
V = h × s(s – a)(s – b)(s – c))
a, b & c = triangle sides
h = height
Volume of a Capsule
V = πr2h + 4 / 3πr3
r = radius
h = height
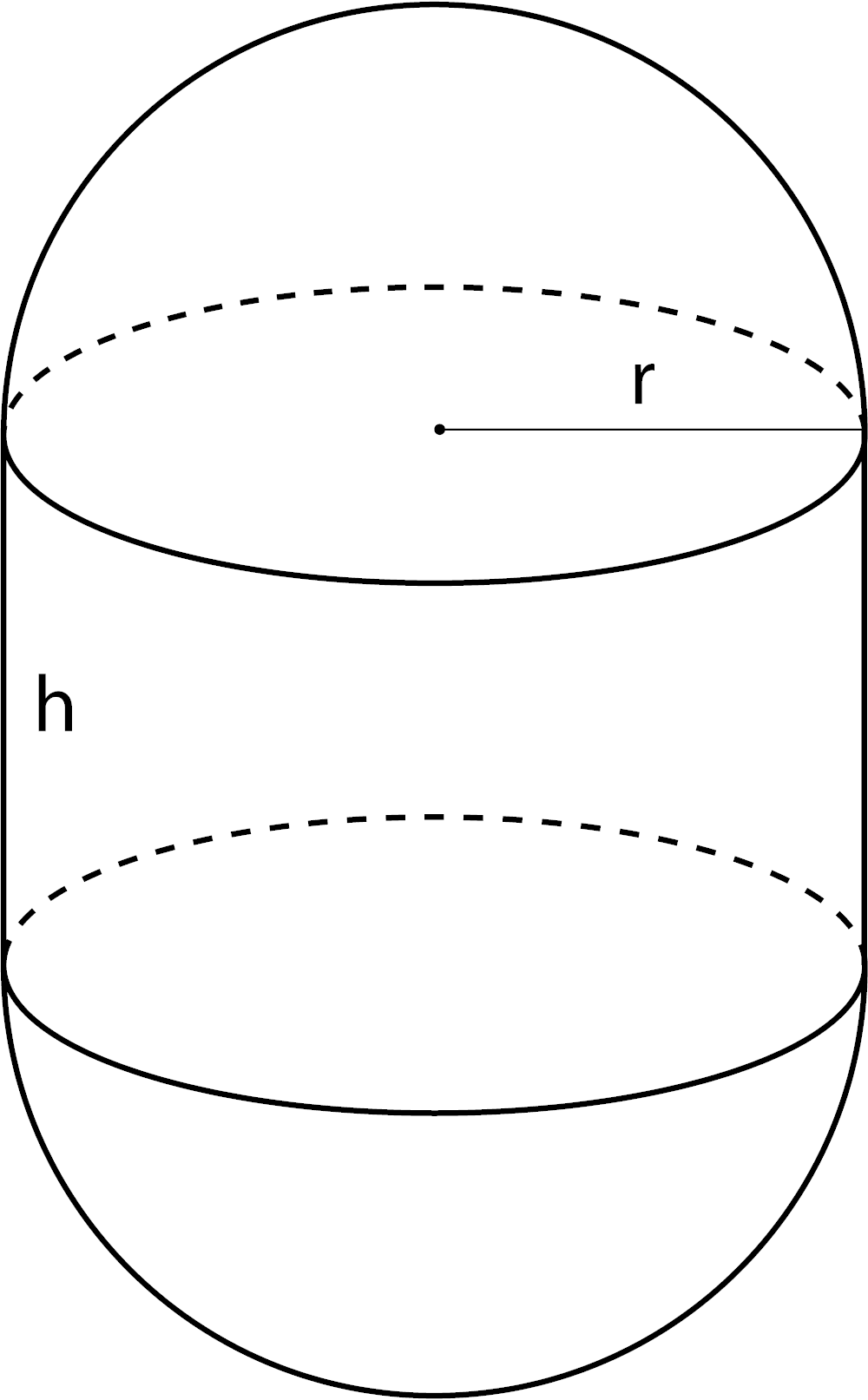
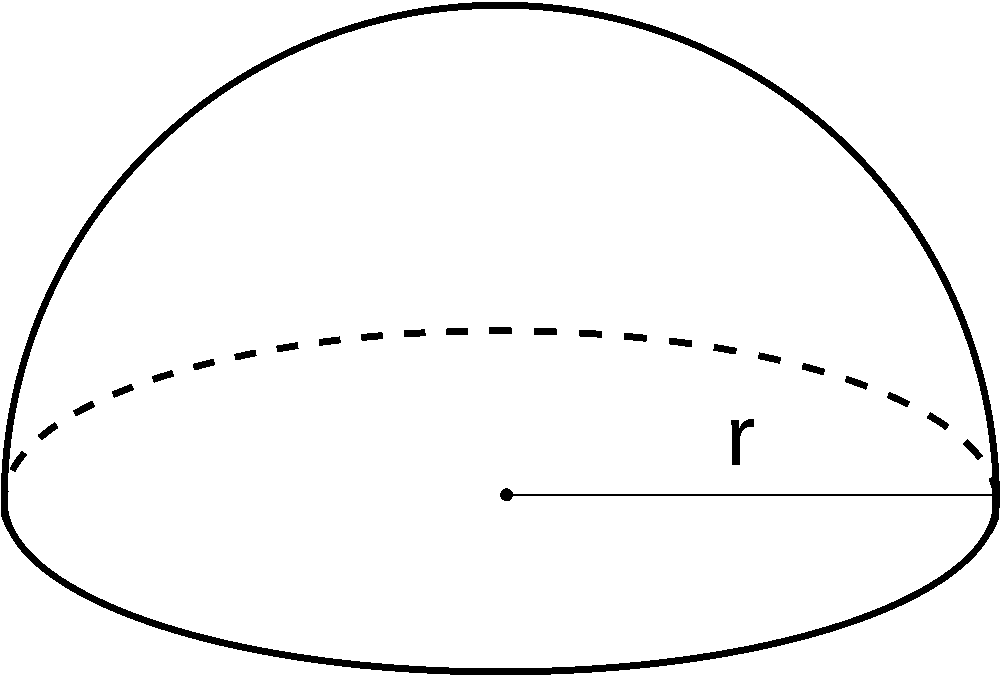
Volume of a Hemisphere
V = 2 / 3πr3
r = radius
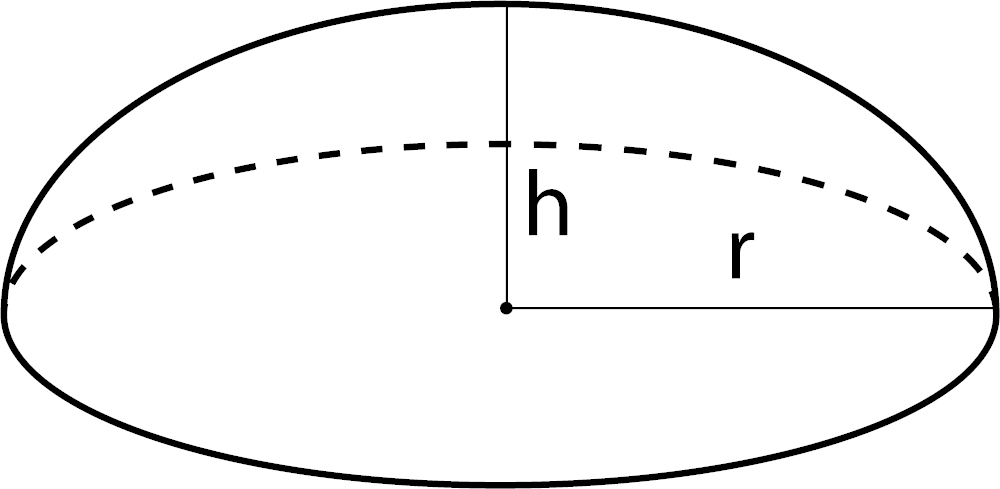
Volume of a Spherical Cap
V = π / 6h(3r2 + h2)
r = radius
h = height
How to Find the Volume of an Irregular Object
The formulas above can be used to calculate regular objects with a defined formula, but many objects are irregular or have no obvious formula. Water displacement is a technique used to find the amount of space an irregular object occupies.
The water displacement technique involves filling a container, that you know the volume of, with water and measuring the amount of water displaced by submerging the irregular object in the water in the container.
For example, fill a container with water and calculate the volume of the water using the formulas above.
Submerge the irregular object in the water and observe that the water level in the container has risen.
Measure the amount of water as before and calculate the volume of the water with the object submerged.
Subtract the initial result by the result after the irregular object was placed in the water to find the volume of the object.
A graduated cylinder is often used for finding the volume of small irregular shaped solids.
Measuring Volume Using Weight
In some cases, you can measure the volume of a fluid or irregular solid material by measuring its mass. If you know the density of the material, you can calculate the volume using its mass with the following formula:
V = m / ρ
where:
V = volume
m = mass
ρ = density
The volume of a material is equal to the mass m divided by its density ρ.
This technique is commonly used to estimate the volume of materials like gravel or water.
Volume Measurement Tips
One important consideration when measuring volume is to take all measurements using the same unit of measure. If your measurements are in different units, convert each measurement to the unit you want the results in.
Use our length converter to convert your measurements to a consistent unit. You can also use our volume converter to convert your result to another unit of measure.
Common Volume Measurements
| Cubic Inch | Cubic Foot | Cubic Yard | Cubic Centimeter | Cubic Meter | |
|---|---|---|---|---|---|
| 1 Cubic Inch = | 1 in3 | 0.000579 ft3 | 0.000021434 yd3 | 16.3871 cm3 | 0.000016387 m3 |
| 1 Cubic Foot = | 1,728 in3 | 1 ft3 | 0.037037 yd3 | 28,317 cm3 | 0.028317 m3 |
| 1 Cubic Yard = | 46,656 in3 | 27.000049 ft3 | 1 yd3 | 764,555 cm3 | 0.764555 m3 |
| 1 Cubic Centimeter = | 0.061024 in3 | 0.000035315 ft3 | 0.000001308 yd3 | 1 cm3 | 0.0000010 m3 |
| 1 Cubic Meter = | 61,024 in3 | 35.314725 ft3 | 1.30795 yd3 | 1,000,000 cm3 | 1 m3 |
You might also be interested in our surface area calculator to find the surface area of a shape.
Frequently Asked Questions
What does volume tell us about an object?
Volume tells us the amount of space an object takes up.
Why is volume cubed?
Volume is measured in cubic units because it is measured using three dimensions. All three dimensions must be multiplied to get the volume.
Why is the volume of sphere 4/3πr³?
Since a sphere is three-dimensional the formula has to be cubed.
How is volume used in real life?
Volume is used in real life to find how much water is needed to fill a swimming pool or a fish tank. Another example would be finding the volume of a gasoline tank so that a car manufacturer would know how much gasoline the tank will hold.
Is volume the same as weight?
No, volume is not the same as weight. Volume is the amount of space an object takes up, while weight is the heaviness of the object.